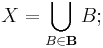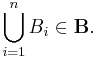Bornological space

In mathematics, particularly in functional analysis, a bornological space is a type of space which, in some sense, possesses the minimum amount of structure needed to address questions of boundedness of sets and functions, in the same way that a topological space possesses the minimum amount of structure needed to address questions of continuity.

Bornological sets

Let X be any set. A bornology on X is a collection B of subsets of X such that

• B is a covering of X, i.e.

• B is stable under inclusions, i.e. if B ∈ B and A ⊆ B, then A ∈ B;
• B is stable under finite unions, i.e. if B₁, ..., B_n ∈ B, then

Elements of the collection B are called bounded sets and the pair (X, B) is called a bornological set.

Examples

• For any set X, the discrete topology of X is a Bornology.
• For any set X, the set of finite (or countably infinite) subsets of X is a Bornology.
• For any topological space X, the set of subsets of X with compact closure is a Bornology.

Bornological spaces in functional analysis

In functional analysis, a bornological space is a locally convex space X such that every semi-norm on X which is bounded on all bounded subsets of X is continuous, where a subset A of X is bounded whenever all continuous semi-norms on X are bounded on A.

Equivalently, a locally convex space X is bornological if and only if the continuous linear operators on X to any locally convex space Y are exactly the bounded linear operators from X to Y.

This gives a connection to the above definition of a bornology. Every topological vector space X gives a bornology on X by defining a subset 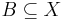to be bounded iff for all open sets 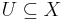containing zero there exists a 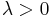with 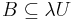. A locally convex X is bornological iff its topology can be recovered from its bornology in a natural way.

For example, any metrisable locally convex space is bornological. In particular, any Fréchet space is bornological.

Given a bornological space X with continuous dual X′, then the topology of X coincides with the Mackey topology τ(X,X′). In particular, bornological spaces are Mackey spaces.

References

• Hogbe-Nlend, Henri (1977). Bornologies and functional analysis. Amsterdam: North-Holland Publishing Co.. pp. xii+144. ISBN 0-7204-0712-5. MR0500064. 
• H.H. Schaefer (1970). Topological Vector Spaces. GTM. 3. Springer-Verlag. pp. 61–63. ISBN 0-387-05380-8.